[자료구조] 비선형 자료구조 - 힙 (Heap)

1. 힙 (Heap) 이란 무엇일까

---

힙은 완전 이진트리의 형태로 최대, 최솟값을 빠르게 찾아내는데 유용하다. 부모-자식 간 (레벨 별) 정렬은 보장하고, 형제간의 정렬은 보장하지 않기 때문에 반정렬 상태 (정렬되지 않은 상태) 이며, 중복값이 허용된다. 트리 구조를 가지고 있기 때문에 삽입/삭제 시간복잡도는 O(logN) 이다. 힙 자료구조는 보통 배열을 사용하며 0번째 인덱스는 계산을 편하게 하기 위해 사용하지 않는다. 즉, 루트노드의 인덱스가 1이다. 부모 자식간의 인덱스 관계는 부모인덱스가 N일 때, 왼쪽 자식은 2N 오른쪽 자식은 2N+1 을 가진다. 힙은 최소 힙 (Min Heap), 최대 힙 (Max Heap) 이 있다. 

 

 

 

---

 

 

 

(1) 이진트리 (Binary Tree) / 완전 이진 트리 (Complete Binary Tree)

• 이진트리 : 모든 노드들이 둘 이하의 자식을 가진 트리, 각 노드는 좌, 우를 구분한다.

왼쪽은 이진트리구조가 아니고 오른쪽은 이진 트리 구조이다.

 

 

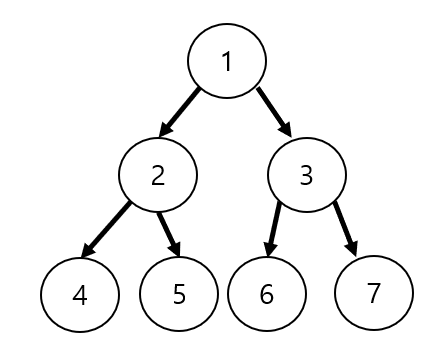
• 완전 이진 트리 : 마지막 레벨을 제외하고 노드들이 가득 차 있는 이진 트리 (자식 노드가 한개만 존재할 경우, 왼쪽부터 채워져야 한다.)

 

 

 

---

 

 

(2) 최소 힙(Min Heap) / 최대 힙 (Max Heap)

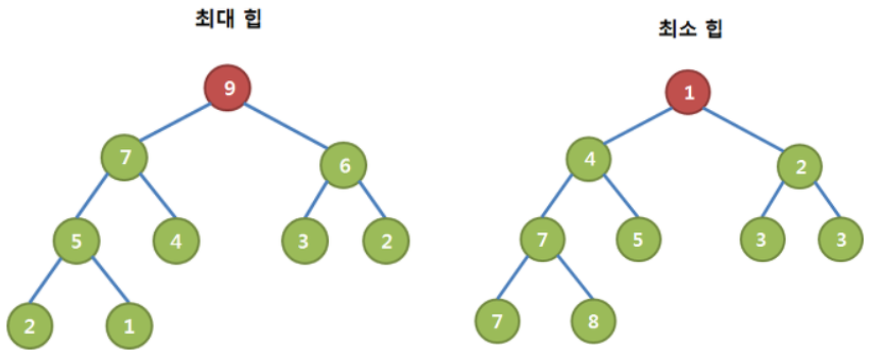
• 최소힙 : 부모노드값이 자식노드의 값보다 작은 형태로 만들어진 완전이진트리, 루트노드에 항상 가장 작은 값 존재
• 최대힙 : 부모노드 값이 자식노드의 값보다 큰 형태로 만들어지는 완전 이진 트리, 루트노드에 항상 가장 큰 값 존재

 

 

 

 

 

---

 

 

 

2. 최소 힙의 삽입 / 삭제 과정

---

• 최소 힙의 삽입 과정

 

 

 

 

 

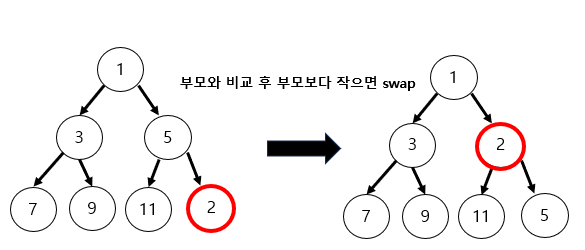
• 최소 힙의 삭제 과정
  • 최소힙은 삭제할 때 최상위 노드를 반환하며 삭제한다.
  • 최상위 노드를 삭제 후 가장 마지막에 위치한 노드를 루트노드로 위치시킨다. 
  • 더 작은 자식노드와 비교하며 작으면 swap 하는 것을 반복한다.

 

 

---

 

 

 

 

• 최대 힙의 삽입 과정

 

 

 

 

 

 

• 최대 힙의 삭제 과정

 

 

 

---

 

 

 

3. 코드로 구현하기

---

ArrayList 를 이용하여 최소 힙 구현

class MinHeap {
	ArrayList<Integer> heap;
    public MinHeap() {
    	this.heap = new ArrayList<>();
        this.heap.add(0);     // index를 맞추기 위함
    }
    public void insert(int data) {
    	heap.add(data);
        
        int cur = heap.size() - 1;     // 방금 추가한 데이터의 인덱스 값
        while(cur > 1 && heap.get(cur/2) > heap.get(cur)) {
        	int parentVal = heap.get(cur/2);
            heap.set(cur/2, data);
            heap.set(cur, parentVal);
            
            cur = cur / 2;
        }
    }
    public void printTree() {
    	for (int i = -; i<this.heap.size();i++) {
        	System.out.print(this.heap.get(i) + " ");
        }
        System.out.println();
    }
    public Integer delete() {
    	if (heap.size() == 1) {
        	System.out.println("Heap is Empty!");
            return null;
        }
        int target = heap.get(1);
        
        heap.set(1,heap.get(heap.size() - 1));    //루트 데이터 값을 가장 마지막에 위치한 노드의 데이터 값으로 변경
        heap.remove(heap.size() - 1);
        
        int cur = 1;
        while (true) {
        	int leftIdx = cur * 2;
            int rightIdx = cur * 2 + 1;
            int targetIdx = -1;
            
            if (rightIdx < heap.size()) {    // 자식이 두개일 때
            	targetIdx = heap.get(leftIdx) < heap.get(rightIdx) ? leftIdx : rightIdx;
            } else if (leftIdx < heap.size()) {    //왼쪽 자식만 존재할 때
            	targetIdx = leftIdx;
            } else {    // 자식이 없을 때
            	break;
            }
            if (heap.get(cur) < heap.get(targetIdx)) {
            	break;
            } else {
            	int parentVal = heap.get(cur);
                heap.set(cur,heap.get(targetIdx));
                heap.set(targetIdx, parentVal);
                cur = targetIdx;
            }
        }
        return target;
    }
}

 

 

 

---

 

 

 

ArrayList 를 이용하여 최대 힙 구현

class MaxHeap {
	ArrayList<Integer> heap;
    public MaxHeap() {
    	this.heap = new ArrayList<>();
        this.heap.add(0);
    }
    public void insert(int data) {
    	heap.add(data);
        int cur = heap.size() - 1;
        while(cur > 1 && heap.get(cur/2) < heap.get(cur)) {
        	int parentVal = heap.get(cur/2);
            heap.set(cur/2, data);
            heap.set(cur, parentVal);
            cur = cur / 2;
        }
    }
    public void printTree() {
    	for(int i =0;i < this.heap.size(); i++) {
        	System.out.print(this.heap.get(i) + " ");
        }
        System.out.println();
    }
    public Integer delete() {
    	if (heap.size() == 1) {
        	System.out.println("Heap is Empty!");
            return null;
        }
        int target = heap.get(1);
        
        heap.set(1,heap.get(heap.size() -1));
        heap.remove(heap.size() - 1);
        
        int cur = 1;
        while(true) {
        	int leftIdx = cur * 2;
            int rightIdx = cur * 2 + 1;
            int targetIdx = -1;
            
            if (rightIdx < heap.size()) {
            	targetIdx = heap.get(leftIdx) > heap.get(rightIdx) ? leftIdx : rightIdx;
            } else if (leftIdx < heap.size()) {
            	targetIdx = leftIdx;
            } else {
            	break;
            }
            if (heap.get(cur) > heap.get(targetIdx)) {
            	break;
            } else {
            	int parentVal = heap.get(cur);
                heap.set(cur,heap.get(targetIdx));
                heap.set(targetIdx, parentVal);
                cur = targetIdx;
            }
        }
        return target;
    }
}